Discover your earning potential
Do you know what you should be paid? Payscale for people is the go-to salary tool for assessing the worth of your job-skills on the open market.
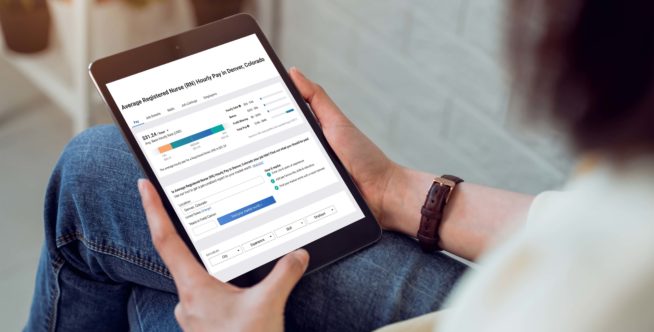
Know your market worth with a personalized salary report
The value of your professional skills in today’s job market is based on a range of evolving factors. Payscale offers unlimited access to tools individuals can use to help negotiate better compensation and benefits. Generate your salary report now.
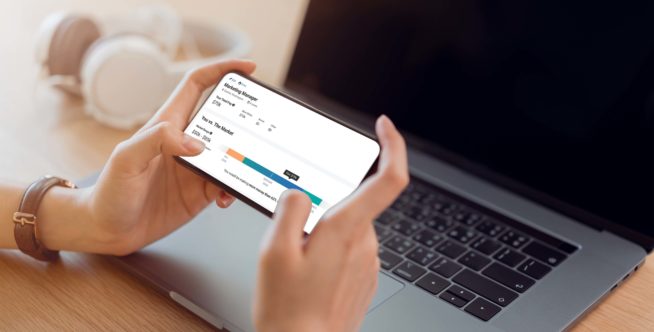
Advance your career with salary and compensation research
The ability to seek and discover in-depth salary data for specific jobs, employers, schools, and more can provide you with the vision to move your career forward with clarity. Visit the Payscale Salary Data & Career Research Center to learn more.
Maximize your wages with insights from
the world’s largest salary database

Research, strategize, negotiate. Our complimentary Salary Negotiation Guide is a vital resource for prepping for your next salary negotiation.

Considering a relocation? Take advantage of our Cost-of-Living Calculator to compare costs for different cities based on your annual salary.

Career questions or compensation uncertainty? Weigh the relationship between jobs and salaries with our real-time Career Growth Planner.
Could your business use
the power of pay?
Explore how Payscale’s compensation solutions
help employers get pay right.
Let Payscale jump-start
your job search
Visit our real-time Job Search engine for
opportunities in your field.





